Sidebar
Table of Contents
CineSat Map Projections
Overview
CineSat provides you with the 63 most frequently used map projections. This ensures that you can read in image data from virtually any standard map format and provide to your clients nicely tailored views of your weather products.
| CineSat Projection Capabilities | |
|---|---|
| • Palette of 63 map projections | ♦ 10 azimuthal projections |
| ♦ 42 cylindrical projections | |
| ♦ 10 conical projections | |
| ♦ 1 miscellaneous projection | |
| • User-configurable Map Parameters | |
| • Spherical and Ellipsoidal Earth Models | |
| • Resampling: Nearest Neighbor, Bi-linear, and Bi-cubic Splines | |
CineSat supports projections onto planes, cylinders, and cones. For each projection surface you may choose among three basic projection properties:
- equi-distant
- equal-area (equivalent) and
- conformal (equal-angles, shape preserving)
Azimuthal projections
Azimuthal projections map the Earth onto either a tangent plane or an intersecting plane (NPOL and SPOL).
The projection planes are in special pose for the NPOL, SPOL, and GEOSAT projections. For all other azimuthal maps you can select the projection plane by specifying the tangent point's longitude and latitude.
CineSat provides you with the following azimuthal map projections:
| Classic perspective azimuthal projections | E/S* | |
|---|---|---|
| ORTHO | orthographic projection | S |
| STEREO | stereographic projection (conformal) | S |
| GNOMONIC | central (gnomonic) projection | S |
| NPOL | polar-stereographic projection North (conformal) | E |
| SPOL | polar-stereographic projection South (conformal) | E |
* The last column indicates the applied earth model: S =Sphere, E = Ellipsoid
Classic perspective projections
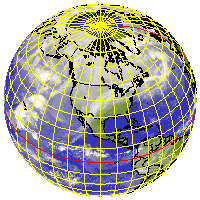
CineSat's ORTHO, STEREO, and GNOMONIC projections are simple perspective projections onto a tangent plane. These projections use a sphere model of the earth. Stereographic projections are conformal.

ORTHO projection onto a North pole tangent plane
STEREO projection onto a North pole tangent plane

GNOMONIC projection onto a North pole tangent plane
New York and Vienna centered orthographic projections, and a stereographic view of New York (rightmost) - all built from an infra-red composite of 5 satellites:
Polar-stereographic projections
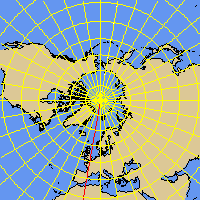
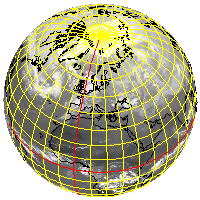
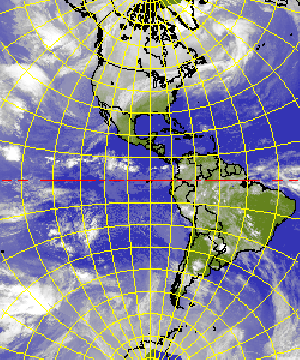
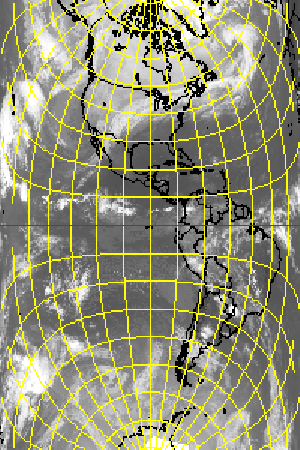
The NPOL and SPOL projections are a special case of a stereographic map. The projection plane intersects the earth at a given standard parallel (including the special case of a tangent plane in the North or South pole). The projections are conformal and preserve true scale along the standard parallel. NPOL and SPOL use an ellipsoidal model of the earth.

NPOL projection
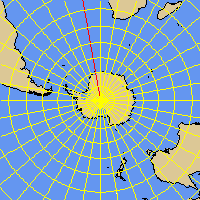
SPOL projection
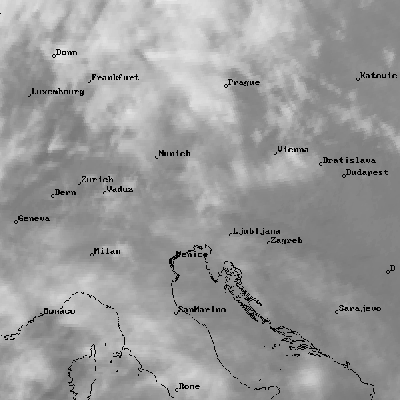
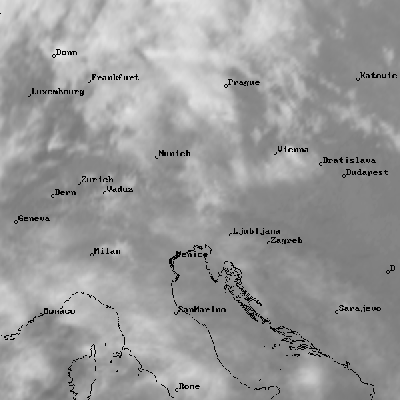
Polar-stereographic projection of the European region;
IR cloud image together with a land/sea background, geographical net and the major European cities drawn as overlay:
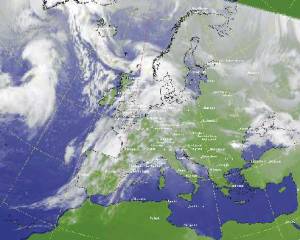
Satellite perspective projections
CineSat provides you with two satellite perspective projections - VPERSPECT and GEOSAT.
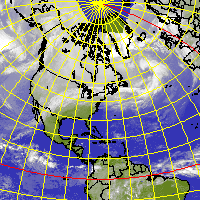
The GEOSAT projection is the standard map used for earth disk images from geostationary meteorological satellites. GEOSAT uses an ellipsoidal model of the earth. The projection plane has its tangent point in the sub-satellite point on the equator. The satellite is the projection center.
GMS GEOSAT projection
Meteosat GEOSAT projection
GOES-E GEOSAT projection
The next image shows a Meteosat-7 B-format image (European region) in native GEOSAT projection:

With VPERSPECT, the projection center can be in any point above the earth surface (not only above the equator). The Vertical Near-Sided Perspective projection (VPERSPECT) uses a spherical earth model.
The following images show a perspective view of the North pole and of Vienna from a distance of 36.000 km:

Equi-distant and equal area projections
EDAP (equi-distant azimuthal projection) and LAZIMUTH (Lambert's azimuthal equal area projection) are no simple perspective projections, but have been mathematically constructed to provide equi-distant and equal area maps, respectively. They use a spherical model of the earth.
The LAZIMUTH projection is a generalization of the ETAP (equivalent transverse azimutal) projection of previous releases.

EDAP - equi-distant azimuthal projection
LAZIMUTH - Lambert's azimuthal equal area projection
Transverse EDAP projection
Oblique EDAP projection
Hammer - a pseudo-azimuthal projection of the world
HAMMER is a modified azimuthal equal-area projection that shows a map of the full earth. You can of course choose any center meridian for this projection.
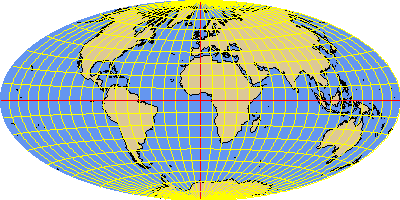
Cylindrical projections
Cylindrical projections map the earth onto a cylinder which either touches the globe along the equator or intersects it at a given standard parallel. The MERCATOR and MILLER projections use an ellipsoidal earth model, all other cylindrical projections take the sphere model.
CineSat provides you with the following 42 cylindrical projections:
| Equi-distant cylindrical projections | E/S* | |
|---|---|---|
| EQUIRECT | equi-distant rectangular projection | S |
| PCARREE | plate carrée (equi-distant square projection , Plattkarte); fixed standard parallel at 0° | S |
| GALLISO | Gall's isographic projection, std parallels at +/-45° | S |
| Equal-area cylindrical projections | E/S* | |
|---|---|---|
| ISOCYL | isocylindrical projection | S |
| LAMBCYL | Lambert's cylindrical projection, std parallel at 0° | S |
| BEHRMANN | Behrmann projection, std parallels at +/-30° | S |
| TRYSTAN | Trystan projection, std parallels at +/-37.383° | S |
| PETERS | Peters projection, std parallels at +/-44.138° | S |
| GALLORTHO | Gall's orthographic projection, std parallels at +/-45° | S |
| BALTHASART | Balthasart projection, std parallels at +/-50° | S |
| Conformal & related cylindrical projections | E/S* | |
|---|---|---|
| MERCATOR | Mercator's conformal cylindrical projection | E |
| MILLER | Miller's projection | E |
| Perspective cylindrical projections | E/S* | |
|---|---|---|
| GNOMOCYL | gnomonic (central) cylindrical perspective | S |
| GALLSTEREO | Gall's stereographic cylindrical projection | S |
| Transverse cylindrical projections | E/S* | |
|---|---|---|
| CASSINI | transverse plate carrée (equi-distant) | S |
| TISOCYL | transverse iso-cylindrical (equal area) | S |
| TMERCATOR | transverse mercator (conformal) | S |
| Pseudo-cylindrical projections | E/S* |
|---|---|
| ECKERT3, ECKERT4, ECKERT5, GOODE, IGOODE, KAVRAISKY7, MERCSAN, MOLLWEIDE, PUTNINS1, PUTNINS2, PUTNINS3, PUTNINS3P, PUTNINS4P, PUTNINS5, PUTNINS5P, PUTNINS6, PUTNINS6P,ROBINSON, WAGNER2, WAGNER3, WAGNER4, WAGNER6, WAGNER7, WERENSKIOLD1, WINKEL1 | S |
* The last column indicates the applied earth model: S =Sphere, E = Ellipsoid
Equi-distant cylindrical projections
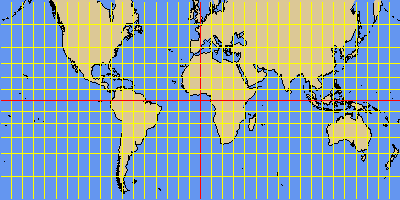
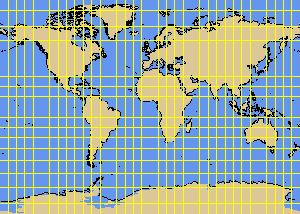
EQUIRECT is the simpliest projection type. It maps the longitude and latitude to a rectangular coordinate system. This projection is frequently used for thematic maps and digital elevation models, since it is very easy to geo-reference.
The standard parallel defines the intersecting cylinder. The following subtypes of the EQUIRECT projection have a fixed standard parallel:
- PCARREE - plate carrée, standard parallel at 0°
- GALLISO - Gall's isographic projection., std. parallels at +/-45°
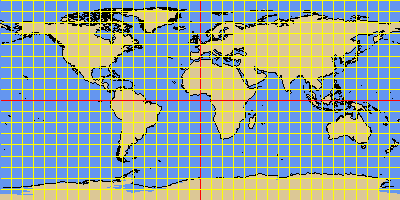
EQUIRECT projection with standard parallel at 0 degree
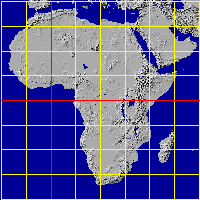
PCARREE projection of Africa
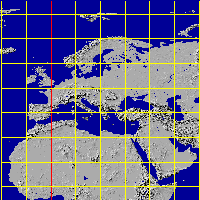
GALLISO projection of Europe
Equal-area cylindrical projections
ISOCYL is an equal area cylindrical projection with several subtypes. The standard parallel defines the intersecting cylinder. Whereas the standard parallel of the intersecting cylinder can be specified with the ISOCYL projection, the following subtypes have a fixed standard parallel:
- LAMBCYL - Lambert's cylindrical projection, std parallel at 0°
- BEHRMANN - standard parallels at +/-30°
- TRYSTAN - standard parallels at +/-37.383°
- PETERS - standard parallels at +/-44.138°
- GALLORTHO - Gall's orthographic projection, std. par. at +/-45°
- BALTHASART - standard parallels at +/-50°
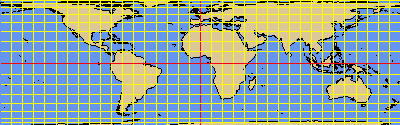
ISOCYL projection with standard parallel at 0°
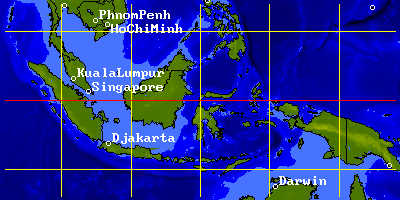
LAMBCYL projection of Indonesia
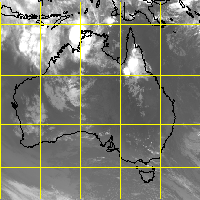
BEHRMANN projection of Australia
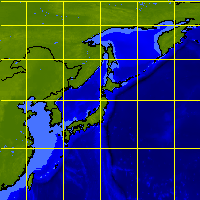
TRYSTAN projection of Japan
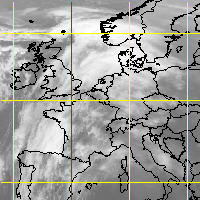
GALLORTHO projection of Europe
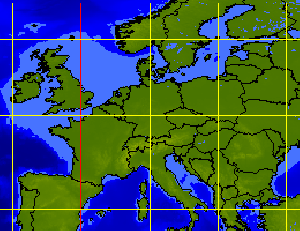
PETERS projection of Europe

BALTHASART projection of Canada
Mercator and Miller projections
Mercator's conformal cylindrical projection and the Miller projection are both very popular for world maps. The MILLER projection has been derived from MERCATOR to reduce the exaggeration of polar areas (see example maps below). Both projection types support an ellipsoidal earth model.
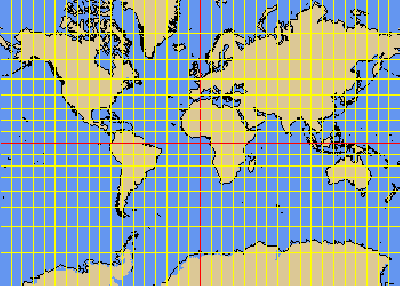
MERCATOR projection
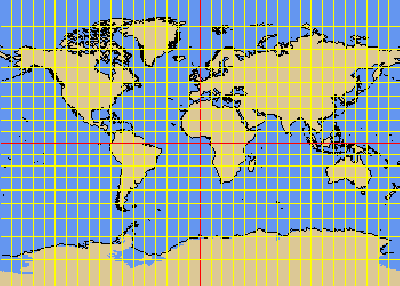
MILLER projection
Perspective cylindrical projections
CineSat completes its range of true cylindrical projections by the following two perspective projections:
- GNOMOCYL - gnomonic (central) cylindrical perspective
- GALLSTEREO - Gall's stereographic cylindrical projection
Gnomonic cylindrical projection
Stereographic cylindrical projection
Transverse cylindrical projections
This projection type maps the sphere onto a cylinder that touches the Earth along a given meridian. Transverse cylindrical projections are often used for areas with a large North-South extent. CineSat supports three transverse cylindrical projections:
- TMERCATOR - transverse mercator (conformal)
- TISOCYL - transverse iso-cylindrical (equal area)
- CASSINI - transverse plate carrée (equi-distant)
TMERCATOR - transverse mercator
TISOCYL - transverse iso-cylindrical
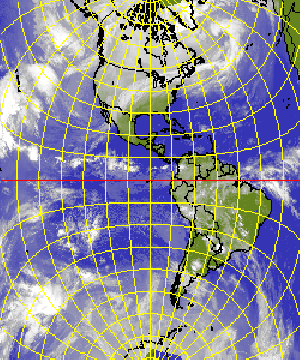
CASSINI - transverse plate carrée
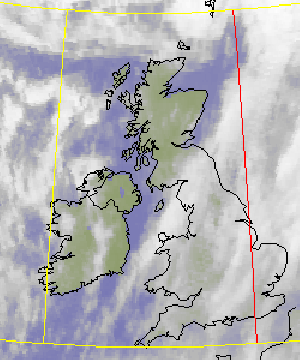
CASSINI projection of Great Britain
Pseudo-cylindrical projections
Pseudo-cylindrical projections are typically used for continental and world maps. They use a spherical earth model.
The following drawings show the 25 pseudo-cylindrical projections provided by CineSat. To make them comparable, all projections have the Greenwich center meridian and show the full globe, but CineSat let's you specify any central meridian and of course any map region and scale.
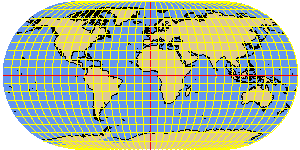
ECKERT3 elliptical
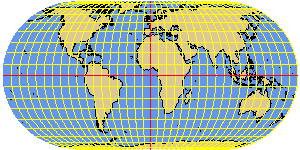
ECKERT4 elliptical equal-area
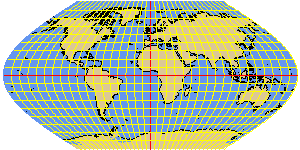
ECKERT5 sinusoidal
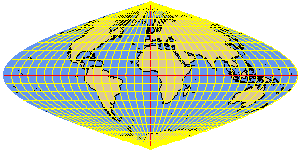
MERCSAN sinusoidal (equal-area) projection or
Mercator-Sanson-Flamsteed
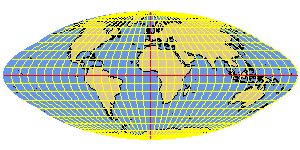
GOODE homolosine equal-area
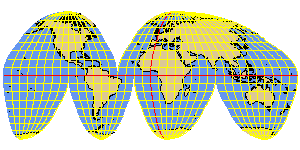
IGOODE interrupted Goode homolosine
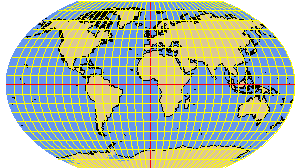
KAVRAISKY7 elliptical
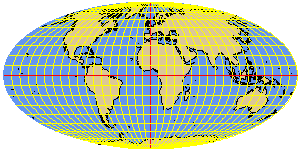
MOLLWEIDE elliptical equal-area
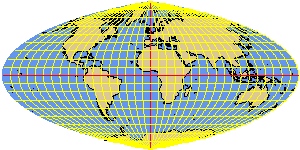
PUTNINS1 elliptical
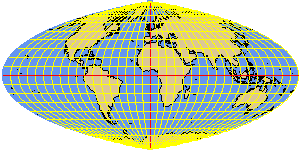
PUTNINS2 elliptical
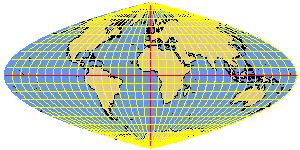
PUTNINS3 parabolic
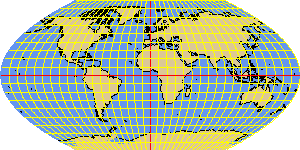
PUTNINS3P parabolic
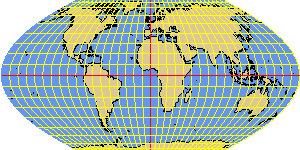
PUTNINS4P parabolic
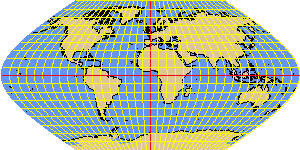
PUTNINS5 hyperbolic

PUTNINS5P hyperbolic
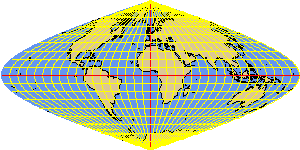
PUTNINS6 hyperbolic
PUTNINS6P hyperbolic
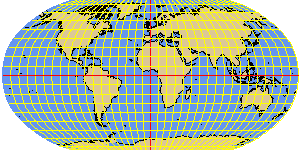
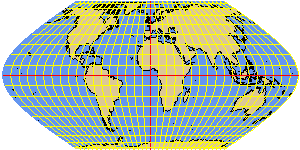
ROBINSON interpolated
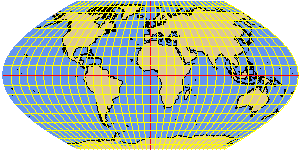
WAGNER2 sinusoidal
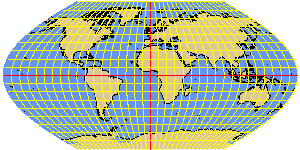
WAGNER3 sinusoidal
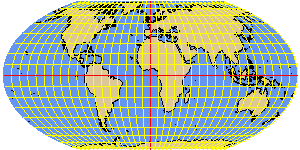
WAGNER4 elliptical equal-area
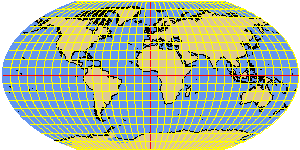
WAGNER6 elliptical
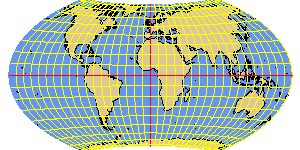
WAGNER7 equal-area
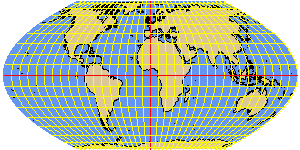
WERENSKIOLD1 parabolic
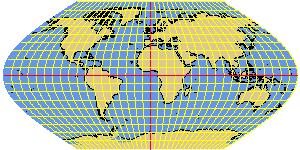
WINKEL1 sinusoidal
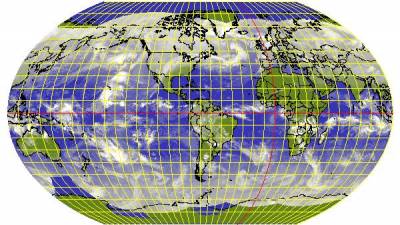
America centered Kavraisky VII projection of the world
Conical projections
Conical projections map the earth either onto a tangent cone or an intersecting cone. The cone's top is located over the North or the South pole. The projection cones can therefore be defined by 1 or 2 intersecting (standard) parallels. Conrical projections are typically used for areas with a large East-West extent.
CineSat provides the following conical projections:
| The 'Great Three' conical projections | E/S* | |
|---|---|---|
| ISLE | equi-distant conical projection by J.N. de l'Isle | E |
| ALBERS | equal area conical projection by H.C. Albers | E |
| LAMBERT | conformal conical projection by J.H.Lambert | E |
| Other conical projections | E/S* | |
|---|---|---|
| EULER | Euler projection | S |
| MURDOCH1 | Murdoch's equi-distant conical projection | S |
| MURDOCH2 | Murdoch II projection | S |
| MURDOCH3 | Murdoch's equi-distant, minimum error projection | S |
| PCONIC | Perspective conic projection | S |
| TISSOT | Tissot projection | S |
| VITKOVSKY1 | Vitkovsky projection | S |
* The last column indicates the applied earth model: S =Sphere, E = Ellipsoid
The 'Great Three' conical projections
The most important conical maps used in meteorology are the ISLE (equi-distant), ALBERS (equal area), and LAMBERT (conformal) projections. All three projections use an ellipsoidal earth model.
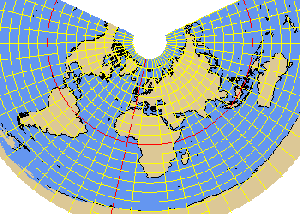
The ISLE projection is an equi-distant conical projection developed by J.N. De l'Isle
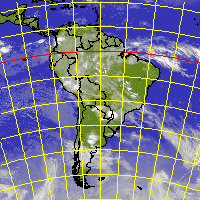
ISLE projection of South America
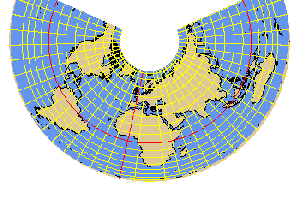
The ALBERS projection is an equal area conical projection developed by H.C. Albers
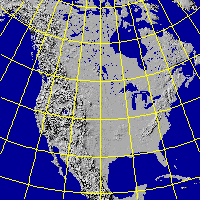
Shaded relief image of North America in ALBERS projection
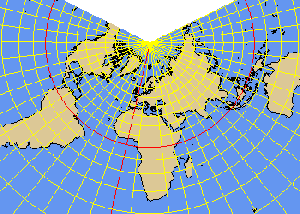
J.H. LAMBERT has developed a widely used, conformal conical projection
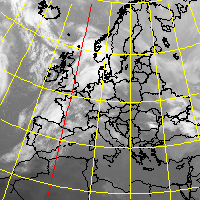
LAMBERT map of Europe
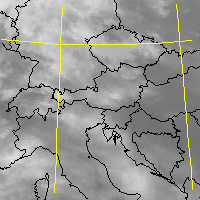
LAMBERT map of Central Europe
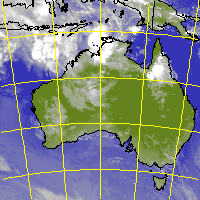
LAMBERT map of Australia
Other conical projections
In addition to the above described 'Great Three', CineSat provides the following 7 conical projections which use a spherical earth model:
- EULER
- MURDOCH1 (equi-distant)
- MURDOCH2
- MURDOCH3 (equi-distant with minimum error)
- PCONIC (perspective conic)
- TISSOT
- VITKOVSKY1
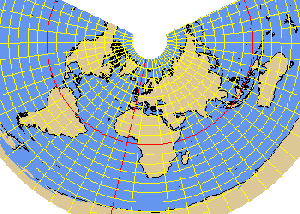
EULER projection
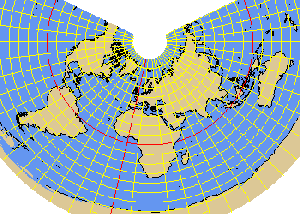
MURDOCH1 projection
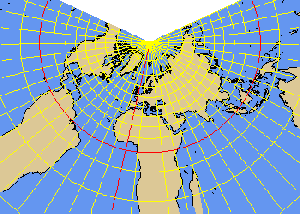
MURDOCH2 projection
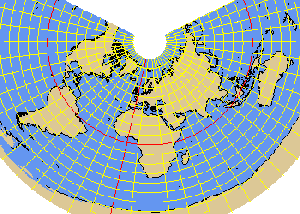
MURDOCH3 projection
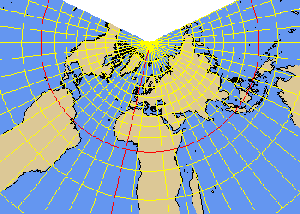
PCONIC perspective conic projection
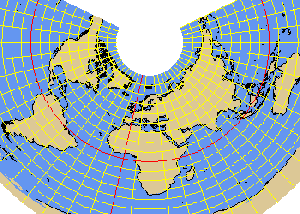
TISSOT projection
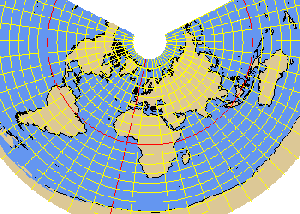
VITKOVSKY1 projection
Miscellaneous projections
Van Der Grinten
CineSat also supports a special projection developed by Van der Grinten (VANDGRINTEN) which maps the full globe into a circle. Some cartographic literature classifies this projection as polyconic.
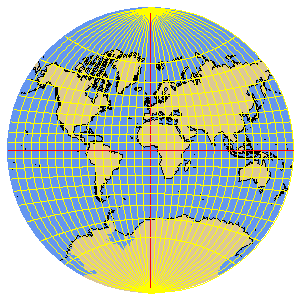
An example VANDGRINTEN world cloud map could look like the image below. You can of course choose any center meridian for this projection:
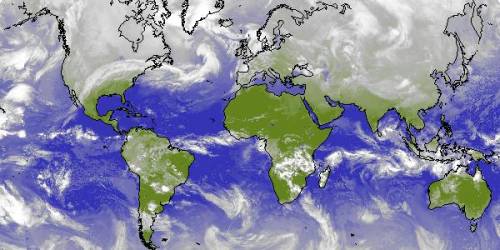
User-configurable Map Parameters
Every projection has a rich set of parameters that can easily be configured to adapt to your image data. A full projection definition consists of
- projection type (e.g. NPOL, MERCATOR, …)
- standard parallel(s)
- center longitude
- satellite height (for perspective satellite views)
- earth radius or spheroid axes
- map area (size and position in the projection plane)
- map scale (pixel resolution)
The projection cylinders and cones will be cut at center longitude + 180° and unfolded into a plane. For the azimuthal projections, you can rotate the projection plane by defining the vertical meridian. For all projections, you can set zoom (resolution) and pan parameters to get your desired region of interest.
All map parameters are stored in projection files with user-defined names. You can then use a projection file name with the PROJECT command to project your images or to generate a map.
Although there are a lot of map configuration options, the usage of these parameters is fairly simple. CineSat comes with a number of pre-defined projections to choose from and start with. Modification of these pre-defined projections is an easy way to develop your own weather views.
Spherical and Ellipsoidal Earth Models
Before mapping Earth coordinates to a projection surface, the irregular 3-dimensional shape of the Earth - the Geoid - is being approximated by the mathematically more handsome spheroid - i.e. either a sphere or an ellipsoid.
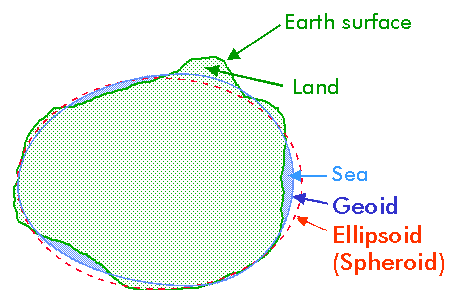
The selection of the best approximating spheroid depends on the mapped region and the required level of cartographic accuracy. CineSat comes with a configuration file that defines the 50 most important standard cartographic spheroids by their names and axes. It also includes the HRIT ellipsoid which had been defined by the Coordination Group for Meteorological Satellites in the HRIT file fomat specifications. Of course, you can use your own sphere or ellipse axes with every CineSat projection.
The ellipsoidal shape of the earth is used by the most important azimuthal, cylindrical, and conical projections. All other projections use the sphere model with a user-defined or a default earth radius.
Standard spheroids significantly increase the interoperability of CineSat with GIS systems and other data sources. They also increase the accuracy of all geographic computations derived from image positions, like point distances and motion vector speeds.
Resampling: Nearest Neighbor, Bi-linear, and Bi-cubic Splines
For every image projection, you can either apply the commonly used nearest neighbor and bi-linear interpolation methods, or a meteorologically tailored bi-cubic spline resampling.
The bi-linear interpolation method is a common resampling technique that is faster than bi-cubic splines but slightly blurs image details. Bi-cubic spline results are sharper and will be your first choice for typical meteorological imaging applications.
The nearest neighbor method will not change pixel values and is recommended for artificial image content, like land masks or cloud images with burnt-in overlays. The method is fast, but has a negative impact on small cloud image structures. The example image below shows the typical nearest neighbor steps in the shape of small cloud cells and cloud borders.
On the other hand, the bi-cubic spline method provided by CineSat is very well suited for producing nice-to-view cloud displays, and for pre-processing images that are intended to be fed to automatic image analysis programs. Small scale cloud structures are being preserved also in projected images and will lead to far better results for all subsequent image texture and object analysis.
CineSat's bi-cubic spline resampling algorithm has been especially developed to accurately rectify and project Meteosat images. The method had been validated and operationally used by the European Space Operations Centre.